Skip to contents

Methods for class localjc

methods_localjc.Rd

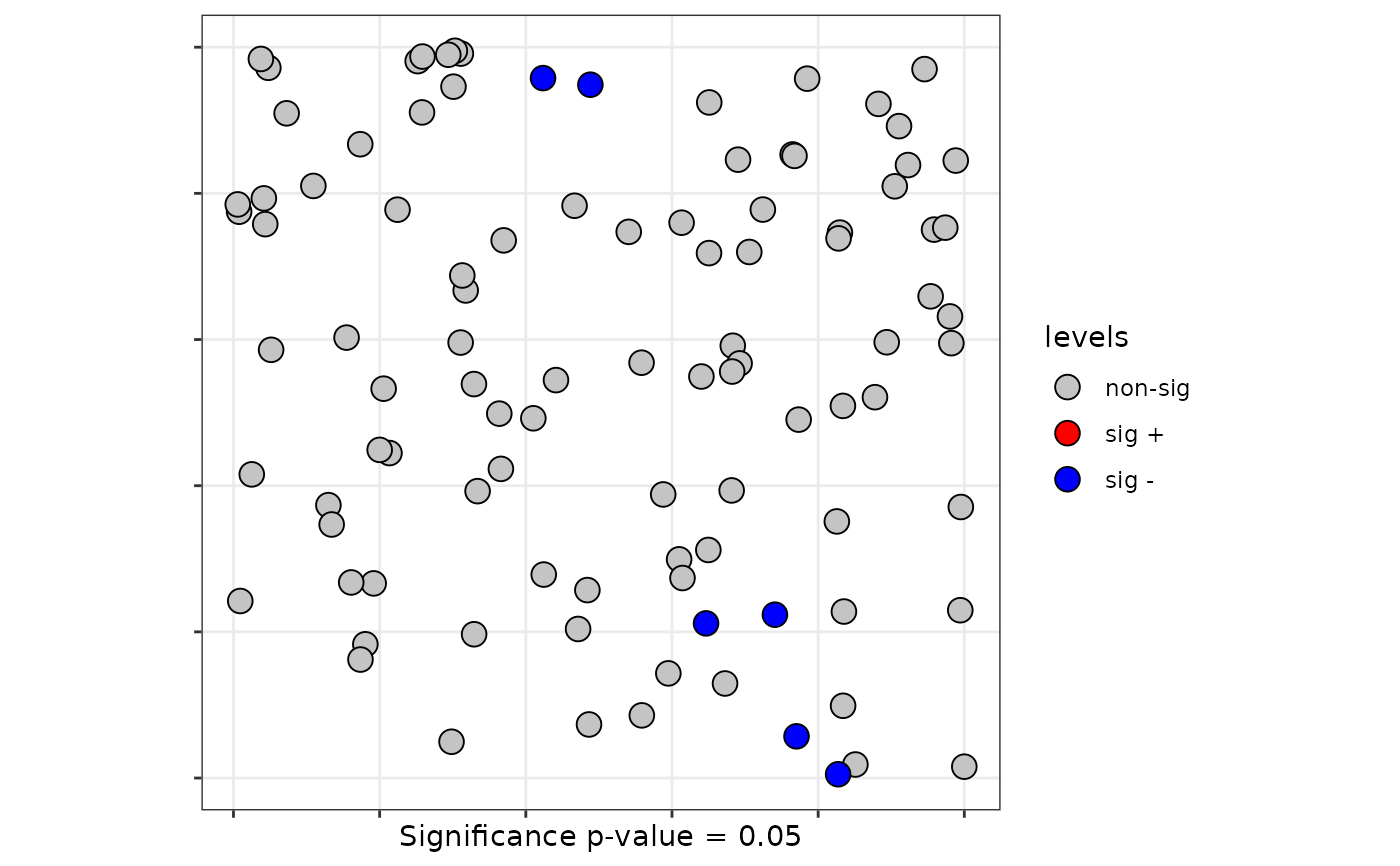
The plot() function allows the user to plot significant observations. The print() function is used to print the number of runs in each localization. Additional information of expected values and standard deviation, z-value ans p-value is prited for each observation.

Usage

# S3 method for localjc
print(x, ...)

# S3 method for localjc
plot(x, ..., sf = NULL, coor = NULL, sig = 0.05)

Arguments

x

a localjc object created by Q.test.

...

further arguments passed to or from other methods.

sf

optional argument for plot() method to include a sf object (default = NULL)

coor

optional argument for plot() method to include coordinates of points (default = NULL)

sig

significant level for each observation in plot() method. Default sig = 0.05

Value

No return value, called for side effects

References

  • Ruiz, M., López, F., and Páez, A. (2021). A test for global and local homogeneity of categorical data based on spatial runs. working paper.

Author

Fernando Lópezfernando.lopez@upct.es
Román Mínguezroman.minguez@uclm.es
Antonio Páezpaezha@gmail.com
Manuel Ruizmanuel.ruiz@upct.es

Examples

# Example 1: Local spatial runs test based on knn
library(lwgeom)
N <- 100
cx <- runif(N)
cy <- runif(N)
x <- cbind(cx,cy)
listw <- spdep::knearneigh(cbind(cx,cy), k = 10)
p <- c(1/6,3/6,2/6)
rho <- 0.5
fx <- dgp.spq(p = p, listw = listw, rho = rho)

# Asymtotic version
lsrq <- local.sp.runs.test(fx = fx, listw = listw, alternative = "less")
print(lsrq)
#>     runs.i      E.i   Std.i    z.value      p.value
#> 1        8 7.183838 1.59988  0.5101392 0.6950230217
#> 2        7 7.183838 1.59988 -0.1149076 0.4542591853
#> 3        7 7.183838 1.59988 -0.1149076 0.4542591853
#> 4        6 7.183838 1.59988 -0.7399544 0.2296638446
#> 5        7 7.183838 1.59988 -0.1149076 0.4542591853
#> 6        7 7.183838 1.59988 -0.1149076 0.4542591853
#> 7        7 7.183838 1.59988 -0.1149076 0.4542591853
#> 8        6 7.183838 1.59988 -0.7399544 0.2296638446
#> 9        7 7.183838 1.59988 -0.1149076 0.4542591853
#> 10       9 7.183838 1.59988  1.1351860 0.8718512930
#> 11       9 7.183838 1.59988  1.1351860 0.8718512930
#> 12       8 7.183838 1.59988  0.5101392 0.6950230217
#> 13       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 14       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 15       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 16       9 7.183838 1.59988  1.1351860 0.8718512930
#> 17       8 7.183838 1.59988  0.5101392 0.6950230217
#> 18       8 7.183838 1.59988  0.5101392 0.6950230217
#> 19       8 7.183838 1.59988  0.5101392 0.6950230217
#> 20       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 21       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 22       8 7.183838 1.59988  0.5101392 0.6950230217
#> 23       4 7.183838 1.59988 -1.9900479 0.0232928297
#> 24       9 7.183838 1.59988  1.1351860 0.8718512930
#> 25      10 7.183838 1.59988  1.7602327 0.9608158220
#> 26       9 7.183838 1.59988  1.1351860 0.8718512930
#> 27       6 7.183838 1.59988 -0.7399544 0.2296638446
#> 28      10 7.183838 1.59988  1.7602327 0.9608158220
#> 29       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 30       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 31       5 7.183838 1.59988 -1.3650011 0.0861263477
#> 32       4 7.183838 1.59988 -1.9900479 0.0232928297
#> 33       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 34       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 35       4 7.183838 1.59988 -1.9900479 0.0232928297
#> 36       6 7.183838 1.59988 -0.7399544 0.2296638446
#> 37       8 7.183838 1.59988  0.5101392 0.6950230217
#> 38       9 7.183838 1.59988  1.1351860 0.8718512930
#> 39       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 40       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 41       8 7.183838 1.59988  0.5101392 0.6950230217
#> 42       8 7.183838 1.59988  0.5101392 0.6950230217
#> 43      11 7.183838 1.59988  2.3852795 0.9914669250
#> 44       5 7.183838 1.59988 -1.3650011 0.0861263477
#> 45       8 7.183838 1.59988  0.5101392 0.6950230217
#> 46       9 7.183838 1.59988  1.1351860 0.8718512930
#> 47       6 7.183838 1.59988 -0.7399544 0.2296638446
#> 48       9 7.183838 1.59988  1.1351860 0.8718512930
#> 49       5 7.183838 1.59988 -1.3650011 0.0861263477
#> 50       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 51       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 52       2 7.183838 1.59988 -3.2401414 0.0005973521
#> 53      10 7.183838 1.59988  1.7602327 0.9608158220
#> 54       8 7.183838 1.59988  0.5101392 0.6950230217
#> 55       8 7.183838 1.59988  0.5101392 0.6950230217
#> 56       9 7.183838 1.59988  1.1351860 0.8718512930
#> 57       8 7.183838 1.59988  0.5101392 0.6950230217
#> 58       4 7.183838 1.59988 -1.9900479 0.0232928297
#> 59       8 7.183838 1.59988  0.5101392 0.6950230217
#> 60       8 7.183838 1.59988  0.5101392 0.6950230217
#> 61       5 7.183838 1.59988 -1.3650011 0.0861263477
#> 62       8 7.183838 1.59988  0.5101392 0.6950230217
#> 63      10 7.183838 1.59988  1.7602327 0.9608158220
#> 64       6 7.183838 1.59988 -0.7399544 0.2296638446
#> 65       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 66       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 67       8 7.183838 1.59988  0.5101392 0.6950230217
#> 68       8 7.183838 1.59988  0.5101392 0.6950230217
#> 69       6 7.183838 1.59988 -0.7399544 0.2296638446
#> 70       8 7.183838 1.59988  0.5101392 0.6950230217
#> 71       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 72       6 7.183838 1.59988 -0.7399544 0.2296638446
#> 73       4 7.183838 1.59988 -1.9900479 0.0232928297
#> 74       6 7.183838 1.59988 -0.7399544 0.2296638446
#> 75       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 76       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 77       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 78       8 7.183838 1.59988  0.5101392 0.6950230217
#> 79       6 7.183838 1.59988 -0.7399544 0.2296638446
#> 80       9 7.183838 1.59988  1.1351860 0.8718512930
#> 81       9 7.183838 1.59988  1.1351860 0.8718512930
#> 82       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 83      11 7.183838 1.59988  2.3852795 0.9914669250
#> 84       9 7.183838 1.59988  1.1351860 0.8718512930
#> 85       5 7.183838 1.59988 -1.3650011 0.0861263477
#> 86       8 7.183838 1.59988  0.5101392 0.6950230217
#> 87       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 88       5 7.183838 1.59988 -1.3650011 0.0861263477
#> 89       9 7.183838 1.59988  1.1351860 0.8718512930
#> 90       8 7.183838 1.59988  0.5101392 0.6950230217
#> 91       5 7.183838 1.59988 -1.3650011 0.0861263477
#> 92       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 93       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 94       7 7.183838 1.59988 -0.1149076 0.4542591853
#> 95       8 7.183838 1.59988  0.5101392 0.6950230217
#> 96       8 7.183838 1.59988  0.5101392 0.6950230217
#> 97       8 7.183838 1.59988  0.5101392 0.6950230217
#> 98       5 7.183838 1.59988 -1.3650011 0.0861263477
#> 99       8 7.183838 1.59988  0.5101392 0.6950230217
#> 100      7 7.183838 1.59988 -0.1149076 0.4542591853
plot(lsrq, sig = 0.05)